{{ post.title }}
글 편집
글 편집 (이전 에디터)
{{ post.author.name }}
完成日期
| Version | {{ post.target_version }} | Product |
{{ product.name }}
|
|---|---|---|---|
| Tutorial/Manual | {{ post.tutorial.upload_filename }} | Attached File | {{ post.file.upload_filename }} |
无制导多管火箭发射初期的动态行为
<客户信息>
• 客户名称:(株)韩华
• 主要工作:火药事业,军工事业,机械航空事业等
<课题>
• 多管无导引火箭发射试弹的初期行为分析
<使用的产品>
• RecurDyn/Professional
• RecurDyn/AutoDesign
<效果>
• 基于MonteCarlo方法导出最满意水平的设计变量
• 确认设计变量对弹初期行为的敏感度
• 通过与未来发射台振动数据的间接比较,确认仿真的可靠性
==========================================================================
防御地区可打击敌人的武器系统的新一代多连弹种包括:制导和无制导有这两种,本案例中基于多物体动力学仿真,运用MonteCarlo方法和Batch模式分析了多管无制导火箭发射时弹的初始行为。
分析中考虑了无导引火箭发射时发射台振动引起的弹初期行为的变化以及由此带来的弹着精度的影响,并掌握了连续发射动特性。并考虑设计变量和运行条件,对弹的初始行为(Pitch,Yaw)进行了分析。
Case Study
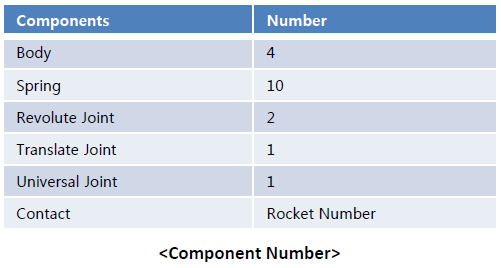
1) 模型设计
模型中假设发射台和车辆,火箭,方位角驱动部为刚体,不考虑推力的错配。此外,未考虑车辆悬架装置,将支承部和高角度液压千斤顶假定为高刚性的弹簧元素,并将发射台振动因素假定为弹后流产生的压力。
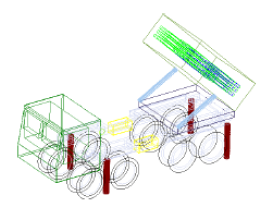
» 弹推力
将体推力数据作为Spline进行了Import,推力Expression使用了AKISPAL(time-发射台稳定时间,0,Sp1,0)。
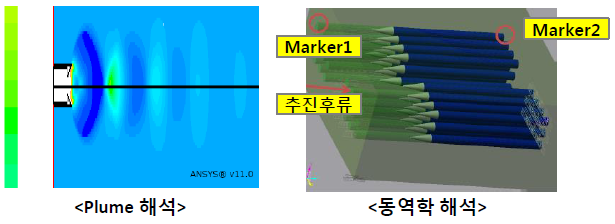
» 弹推进尾流
将由Plume仿真得到的压力值换算为集中力后应用,用IF(DZ(1,2,1):0,0,弹推进后流)-if(DZ(1,2,1)-(弹推进后流有效距离:0,0,弹推进后流)。 作为参考,在这个表达式里,1代表Marker1,2代表Marker2。
2) 设计变量和运用条件
» 设计变量和运用条件的设置
选定影响弹初行为的设计变量和运用条件。设计变量指弹约束解力,发射管长度,支撑千斤顶,运用条件指仰角,方位角,发射间隔。
» 设计条件变量化(发射管长度)
利用了Parametric Point,Parametric Value,Expression和Parametric Point Connector。
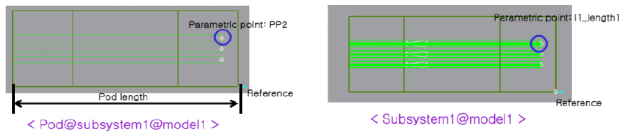
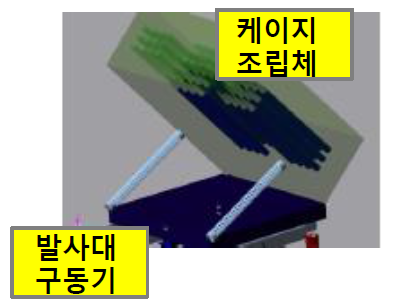
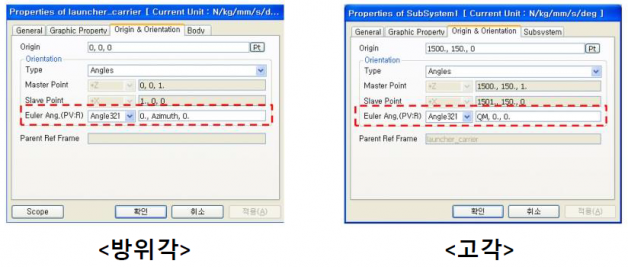
» 运转条件变量化(仰角,方位角)
ㆍ 方位角:将笼形组装体指定为发射台驱动程序的Subsystem,发射台驱动程序启动后笼形组装体也一起旋转。 此外,还指定Euler Angle为Parameter value(V:Azimuth)。
ㆍ 仰角:Euler Angle被指定为Parameter value(V:QM)。
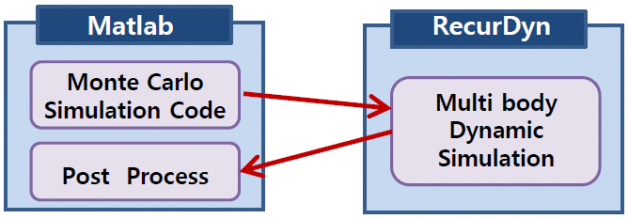
3) 进行过程
» 仿真结果
验证了弹的Pitch Rate,Yaw Rate作为发射台振动参考数据
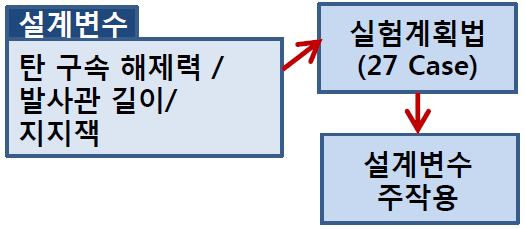
» 设计变量影响分析
3水平完全配置法,实验计划法确定了设计变量的主要作用。
» 考虑运用条件的设计变量影响因素分析
分别将Monte Carlo模拟应用于实验计划法,完全配置法中。
效果
本案例分析了无制导多管火箭发射初期的动态行为,基于MonteCarlo方法得出了最满意水平的设计变量,确定了对弹初行为的设计变量敏感度。此外,通过本案例还表明,今后可以通过与发射台振动数据的间接比较来确定仿真的可靠性。
* 本内容是对2010年RecurDyn User’’s Conference发布资料的整理。